Chào mừng bạn đến với thienvanhoc.edu.vn! Trong bài viết này, chúng tôi sẽ khám phá ba Định luật Kepler – những nguyên lý cơ bản định hình sự hiểu biết của chúng ta về chuyển động của các hành tinh trong hệ Mặt Trời. Định luật Kepler không chỉ là những nguyên tắc thiên văn học mà còn là nền tảng cho các nghiên cứu về lực hấp dẫn và chuyển động trong vũ trụ.
Bằng cách đi sâu vào từng định luật, chúng tôi hy vọng sẽ cung cấp cho bạn những kiến thức thú vị và hữu ích, giúp bạn hiểu rõ hơn về cách thức mà các thiên thể tương tác với nhau. Hãy cùng chúng tôi khám phá những bí ẩn của vũ trụ qua các định luật kỳ diệu này!
Tìm hiểu về định luật Kepler
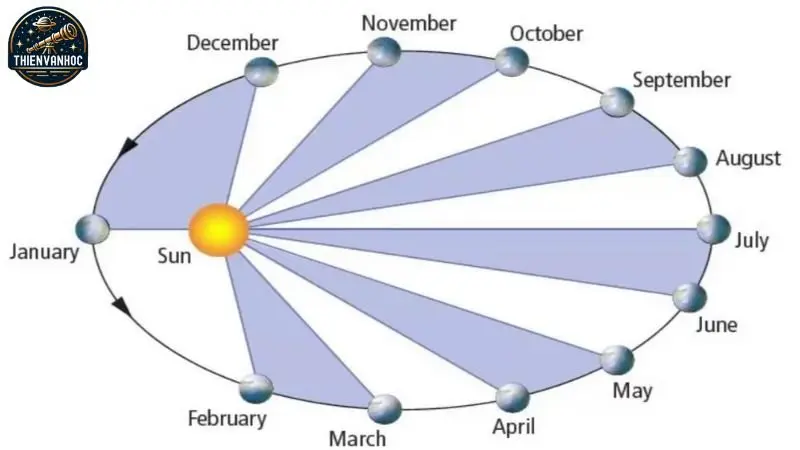
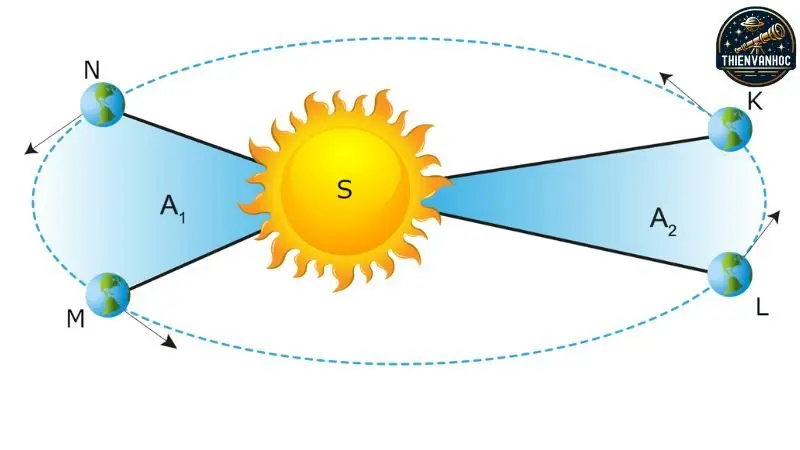
Năm 1609, Kepler xuất bản tác phẩm “Astronomia Nova”, trong đó ông trình bày hai định luật đầu tiên về chuyển động hành tinh, được biết đến ngày nay là các định luật của Kepler. Theo ông, một đường tưởng tượng nối từ một hành tinh đến Mặt trời sẽ quét qua những diện tích bằng nhau trong những khoảng thời gian bằng nhau, bất kể vị trí của hành tinh trên quỹ đạo. Nghĩa là, nếu bạn vẽ một hình tam giác từ Mặt trời đến vị trí của một hành tinh tại một thời điểm cụ thể và đến vị trí của nó sau một khoảng thời gian xác định, thì diện tích của tam giác đó luôn bằng nhau tại mọi vị trí trên quỹ đạo.
Để duy trì diện tích tam giác này không đổi, hành tinh cần phải di chuyển nhanh hơn khi ở gần Mặt trời và chậm hơn khi ở xa Mặt trời. Phát hiện này đã hình thành nên định luật thứ hai của Kepler về chuyển động quỹ đạo và dẫn đến định luật đầu tiên của ông: các hành tinh di chuyển theo quỹ đạo hình elip với Mặt trời nằm tại một tiêu điểm, không phải tại tâm của elip.
Đến năm 1619, Kepler công bố tác phẩm “Harmonices Mundi”, trong đó ông mô tả định luật thứ ba của mình. Định luật này chỉ ra một mối quan hệ toán học chính xác giữa khoảng cách từ một hành tinh đến Mặt trời và thời gian mà nó cần để hoàn thành một vòng quay quanh Mặt trời.
Định luật Kepler thứ nhất – Định luật quỹ đạo
Theo định luật thứ nhất của Kepler, “Tất cả các hành tinh quay quanh Mặt trời theo những quỹ đạo hình elip, với Mặt trời nằm ở một trong các tiêu điểm.” Điểm mà hành tinh tiến gần Mặt trời nhất được gọi là cận nhật, cách Mặt trời khoảng 147 triệu km. Ngược lại, điểm mà hành tinh ở xa Mặt trời nhất được gọi là viễn nhật, cách Mặt trời khoảng 152 triệu km. Một đặc điểm quan trọng của hình elip là tổng khoảng cách từ một hành tinh đến hai tiêu điểm luôn không thay đổi.
Định luật Kepler thứ hai – Định luật diện tích bằng nhau
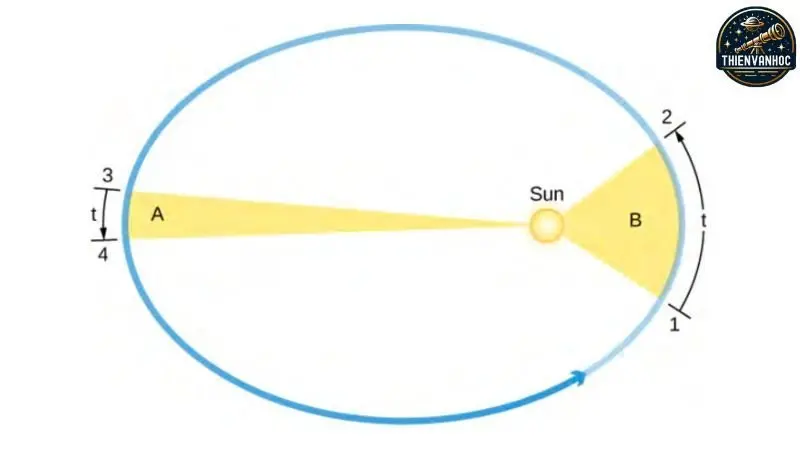
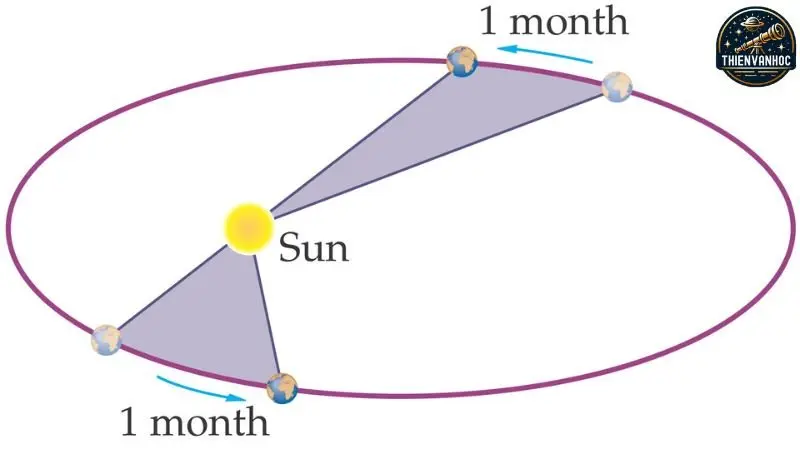
Định luật thứ hai của Kepler phát biểu rằng: “Vectơ bán kính kéo từ Mặt trời đến hành tinh quét qua những diện tích bằng nhau trong những khoảng thời gian bằng nhau.”
Do quỹ đạo hành tinh có dạng hình elip thay vì hình tròn, động năng của hành tinh không ổn định khi nó di chuyển. Hành tinh có động năng lớn hơn khi ở gần Mặt trời (điểm cận nhật) và ít động năng hơn khi ở xa Mặt trời (điểm viễn nhật), dẫn đến tốc độ cao hơn tại điểm cận nhật và tốc độ thấp hơn (vmin) tại điểm viễn nhật. Nếu r là khoảng cách từ hành tinh đến Mặt trời, tại điểm cận nhật là rmin và tại điểm viễn nhật là rmax, thì:
\[ r_{min} + r_{max} = 2a \]
trong đó a là bán trục chính của hình elip.
Sử dụng định luật bảo toàn động lượng góc, định luật này có thể được chứng minh. Tại bất kỳ thời điểm nào, động lượng góc (L) được biểu diễn là:
\[ L = mr^2\omega \]
trong đó m là khối lượng của hành tinh, r là khoảng cách từ hành tinh đến Mặt trời, và ω là vận tốc góc.
Xem xét một diện tích nhỏ ΔA quét được trong một khoảng thời gian ngắn Δt với góc quét là Δθ, độ dài cung của đường đi được tính là rΔθ. Khi đó:
\[ \Delta A = \frac{1}{2}[r \cdot (r \cdot \Delta \theta)] = \frac{1}{2} r^2 \Delta \theta \]
Do đó, tốc độ quét diện tích là:
\[ \frac{\Delta A}{\Delta t} = \frac{1}{2} r^2 \frac{\Delta \theta}{\Delta t} \]
Khi lấy giới hạn Δt → 0, ta có:
\[ \frac{dA}{dt} = \frac{1}{2} r^2 \frac{d\theta}{dt} \]
Với định luật bảo toàn động lượng góc, L là một hằng số, dẫn đến:
\[ \frac{dA}{dt} = \text{Hằng số} \]
Do đó, diện tích quét được trong những khoảng thời gian bằng nhau là một hằng số.
Định luật thứ hai của Kepler cũng có thể được phát biểu là: “Vận tốc quét diện tích của một hành tinh quay quanh Mặt trời theo quỹ đạo hình elip là không đổi, điều này ngụ ý rằng động lượng góc của hành tinh không đổi.” Vì động lượng góc không đổi, mọi chuyển động của hành tinh đều là chuyển động phẳng, là hệ quả trực tiếp của lực trung tâm.
Định luật Kepler thứ ba – Định luật về chu kỳ
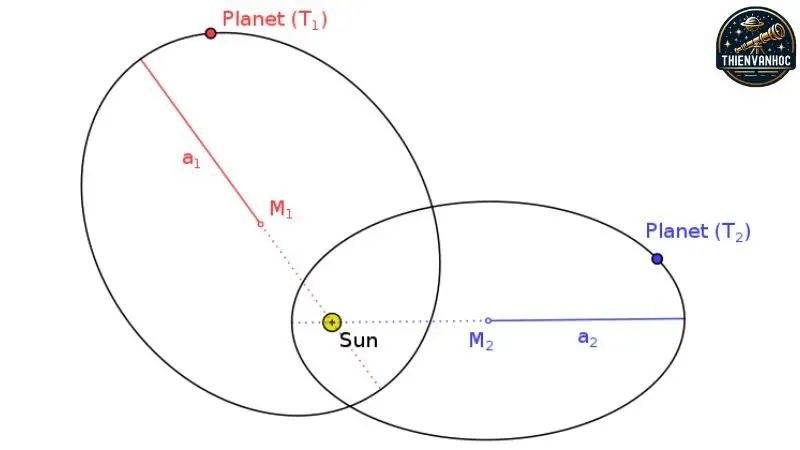
Định luật thứ ba của Kepler, hay còn gọi là định luật chu kỳ, phát biểu rằng: “Bình phương chu kỳ quỹ đạo của một hành tinh quanh Mặt trời theo quỹ đạo hình elip tỉ lệ thuận với lập phương của bán trục lớn của quỹ đạo đó.”
\[ T^2 \propto a^3 \]
Điều này có nghĩa là quỹ đạo của hành tinh càng ngắn thì thời gian để hoàn thành một vòng quay quanh Mặt trời càng ngắn. Khi kết hợp với các phương trình của định luật hấp dẫn và định luật chuyển động của Newton, định luật thứ ba của Kepler được biểu diễn dưới dạng tổng quát hơn như sau:
\[ P^2 = \frac{4 \pi^2}{G (M_1 + M_2)} \cdot a^3 \]
Trong đó:
– \( P \) là chu kỳ quỹ đạo
– \( G \) là hằng số hấp dẫn
– \( M_1 \) và \( M_2 \) là khối lượng của hai vật thể quay quanh nhau
– \( a \) là bán trục lớn của quỹ đạo elip
Như vậy, định luật này không chỉ áp dụng cho các hành tinh quay quanh Mặt trời mà còn có thể áp dụng cho bất kỳ hai vật thể nào trong không gian quay quanh khối tâm chung của chúng, mở rộng tầm hiểu biết về chuyển động quỹ đạo trong vũ trụ.
Khám phá mối liên hệ giữa định luật Newton và định luật Kepler
Các định luật Kepler về chuyển động của hành tinh được hỗ trợ vững chắc bởi định luật của Newton. Theo định luật Newton về chuyển động, một vật thể chỉ có thể thay đổi tốc độ khi có lực tác động lên nó, điều này phù hợp với Định luật Kepler thứ nhất, cho thấy các hành tinh di chuyển theo quỹ đạo elip xung quanh Mặt trời, với Mặt trời tại một trong các tiêu điểm.
Thêm vào đó, theo Định luật thứ hai của Kepler, diện tích quét bởi bán kính vector từ Mặt trời đến hành tinh là không đổi trong các khoảng thời gian bằng nhau, điều này khẳng định sự ổn định của vận tốc diện tích.
Cùng với đó, sự tương ứng giữa Định luật thứ ba của Kepler và Định luật thứ ba của Newton cho thấy lực hấp dẫn giữa Mặt trời và hành tinh tỷ lệ thuận với tích của khối lượng của hai thể này.
Nhờ vậy, sự hợp lý và đầy đủ của ba định luật chuyển động của Newton có thể được thấy rõ qua việc chúng hỗ trợ và mở rộng hiểu biết về các định luật chuyển động hành tinh của Kepler.
Ngày nay chúng ta sử dụng định luật Kepler như thế nào?
Khi Kepler đề xuất ba định luật về chuyển động hành tinh, ông chưa biết đến lực hấp dẫn, yếu tố giữ các hành tinh quay quanh Mặt trời. Tuy nhiên, các định luật của ông đã trở thành nền tảng giúp Isaac Newton phát triển lý thuyết vạn vật hấp dẫn, giải thích lực đằng sau định luật thứ ba của Kepler. Những đóng góp của Kepler là cơ sở quan trọng trong việc hiểu động lực học của hệ Mặt trời và là tiền đề cho các lý thuyết quỹ đạo hành tinh sau này. Tuy nhiên, định luật thứ ba của ông chỉ áp dụng trong phạm vi hệ Mặt trời của chúng ta.
Newton đã mở rộng định luật thứ ba của Kepler, cho phép tính toán khối lượng của bất kỳ hai vật thể nào trong không gian nếu biết khoảng cách giữa chúng và chu kỳ quỹ đạo của chúng. Khám phá quan trọng của Newton là quỹ đạo của các vật thể phụ thuộc vào khối lượng của chúng, điều này dẫn đến việc khám phá lực hấp dẫn.
Phiên bản tổng quát của định luật thứ ba Kepler theo Newton là nền tảng cho hầu hết các phép đo khối lượng của các vật thể xa trong không gian hiện nay. Những ứng dụng này bao gồm việc xác định khối lượng của các mặt trăng quay quanh hành tinh, các ngôi sao quay quanh nhau, khối lượng của các lỗ đen (thông qua các ngôi sao bị ảnh hưởng bởi lực hấp dẫn của chúng), và khối lượng của các ngoại hành tinh (các hành tinh quay quanh các ngôi sao khác ngoài Mặt trời của chúng ta). Nó cũng giúp xác định sự tồn tại của vật chất tối trong thiên hà của chúng ta và các thiên hà khác.
Khi lập kế hoạch quỹ đạo cho tàu vũ trụ và thực hiện các phép đo khối lượng của mặt trăng và hành tinh, các nhà khoa học hiện đại thường sử dụng thêm yếu tố thuyết tương đối của Albert Einstein để đạt được độ chính xác cao cho các phép đo và các chuyến bay vũ trụ.
Tuy vậy, các định luật của Newton vẫn đủ chính xác cho nhiều ứng dụng, và định luật Kepler vẫn là công cụ hữu ích trong việc hiểu cách các hành tinh chuyển động trong hệ Mặt trời của chúng ta.
Ứng dụng định luật Kepler trong tính toán chu kỳ quỹ đạo của hành tinh
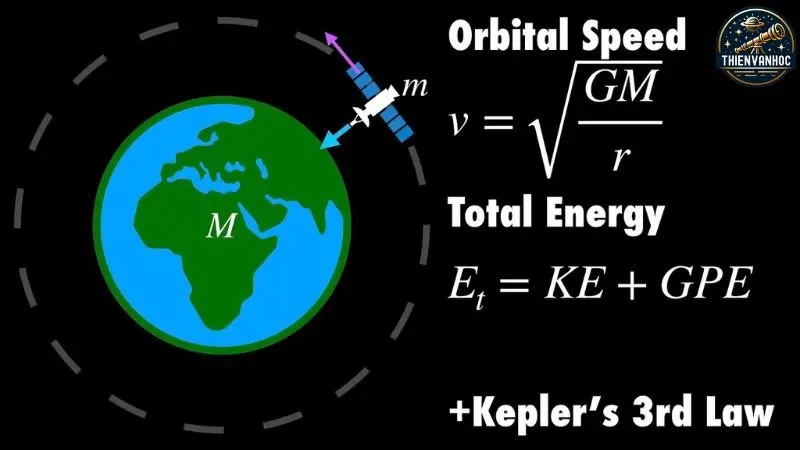
Ví dụ 1: Hãy xem xét một ví dụ về việc tính toán chu kỳ quỹ đạo của một hành tinh dựa trên Định luật Kepler. Giả sử rằng bán kính quỹ đạo của hành tinh này gấp ba lần bán kính quỹ đạo của Trái Đất.
Giải thích bước giải:
Đặt bán kính quỹ đạo của Trái Đất là \( R_e \), và bán kính quỹ đạo của hành tinh là \( R_p \). Chu kỳ quay quanh Mặt Trời của Trái Đất là \( T_e \) và của hành tinh cần tính là \( T_p \).
Thông tin đã cho:
– \( R_p = 3R_e \)
– Chu kỳ của Trái Đất, \( T_e \), là 1 năm.
Áp dụng định luật Kepler thứ ba:
\[ \frac{T_p^2}{T_e^2} = \frac{R_p^3}{R_e^3} \]
Thay thế các giá trị vào công thức:
\[ \frac{T_p^2}{(1 \text{ năm})^2} = \left(3R_e\right)^3 / R_e^3 \]
\[ T_p^2 = 27 \text{ năm} \]
\[ T_p = \sqrt{27 \text{ năm}} = 5,2 \text{ năm} \]
Do đó, chu kỳ quỹ đạo của hành tinh này là khoảng 5,2 năm. Điều này cho thấy hành tinh đó mất 5,2 năm để hoàn thành một vòng quay quanh Mặt Trời.
Ví dụ 2: Xét một hành tinh có bán kính quỹ đạo gấp tám lần bán kính quỹ đạo của Trái Đất. Mục tiêu là xác định chu kỳ quỹ đạo của hành tinh đó.
Quy trình tính toán:
Đầu tiên, áp dụng Định luật thứ ba của Kepler, cho rằng bình phương chu kỳ quỹ đạo tỷ lệ thuận với lập phương của bán kính quỹ đạo:
\[ T^2 \propto R^3 \]
Các giá trị đã biết:
– Bán kính Trái Đất là \( R_e \).
– Chu kỳ quỹ đạo của Trái Đất là \( T_e = 1 \text{ năm} \).
– Bán kính quỹ đạo của hành tinh là \( R_p = 8 R_e \).
Tính toán:
Sử dụng mối liên hệ giữa chu kỳ và bán kính:
\[ \frac{T_p^2}{T_e^2} = \frac{R_p^3}{R_e^3} \]
\[ \frac{T_p^2}{(1 \text{ năm})^2} = (8 R_e)^3 / R_e^3 \]
\[ T_p^2 = 512 \text{ năm} \]
\[ T_p = \sqrt{512 \text{ năm}} = 22,63 \text{ năm} \]
Như vậy, hành tinh này mất khoảng 22,63 năm để hoàn thành một vòng quay quanh Mặt Trời. Điều này cung cấp thông tin quan trọng về đặc điểm quỹ đạo của hành tinh trong hệ Mặt Trời của chúng ta.
Ví dụ 3: Ví dụ này giải quyết việc tính toán diện tích quỹ đạo của Trái Đất dựa trên tỷ số giữa mô men động lượng quỹ đạo quanh Mặt Trời và khối lượng của Trái Đất.
Thông tin đầu vào:
– Tỷ số giữa mô men động lượng quỹ đạo và khối lượng Trái Đất là \(4,4 \times 10^{15} \text{ m}^2/\text{s}\).
– Chu kỳ quỹ đạo của Trái Đất là một năm, tương đương với:
– \(365\) ngày,
– \(365 \times 86400\) giây,
– \(31,536,000\) giây.
Quy trình tính toán:
Diện tích quét qua bởi vector bán kính từ Mặt Trời đến Trái Đất được tính bằng công thức:
\[ \text{dA} = \left(\frac{L}{m}\right) \times \left(\frac{\text{dt}}{2}\right) \]
Thay số liệu vào:
\[ \text{dA} = (4,4 \times 10^{15}) \times (31,536,000 / 2) \text{ m}^2 \]
\[ \text{dA} = 6,938 \times 10^{22} \text{ m}^2 \]
Kết quả là diện tích được quét qua bởi Trái Đất trong một chu kỳ quỹ đạo là khoảng \(6,938 \times 10^{22} \text{ m}^2\). Đây là thông tin quan trọng cho việc hiểu và mô tả chuyển động của Trái Đất quanh Mặt Trời.
Giải đáp các câu hỏi thường gặp về định luật Kepler
Câu hỏi 1: Làm thế nào Newton đã mở rộng lý thuyết về lực hấp dẫn để giải thích chuyển động của các hành tinh?
Newton phát biểu rằng lực hấp dẫn giữa hai vật tỷ lệ nghịch với bình phương khoảng cách giữa chúng, là cơ sở của định luật bình phương nghịch đảo. Điều này cùng với Định luật thứ nhất của Kepler, cho rằng các hành tinh di chuyển theo quỹ đạo elip với Mặt Trời tại một tiêu điểm, hỗ trợ lẫn nhau trong việc mô tả chuyển động của hành tinh.
Câu hỏi 2: Định luật Kepler thứ nhất mô tả hình dạng quỹ đạo của các hành tinh như thế nào?
Định luật thứ nhất của Kepler, hay còn gọi là Định luật quỹ đạo, khẳng định rằng các hành tinh di chuyển xung quanh Mặt Trời theo một đường elip, trong đó Mặt Trời chiếm một trong các tiêu điểm của elip.
Câu hỏi 3: Định luật Kepler thứ hai giải thích sự thay đổi vận tốc của hành tinh trên quỹ đạo như thế nào?
Định luật thứ hai của Kepler chỉ ra rằng diện tích quét bởi bán kính nối từ Mặt Trời đến hành tinh là nhất quán theo thời gian. Do đó, khi hành tinh tiến gần Mặt Trời hơn, nó di chuyển nhanh hơn và chậm lại khi xa hơn.
Câu hỏi 4: Định luật Kepler thứ ba so sánh thời gian hoàn thành quỹ đạo của các hành tinh trên các quỹ đạo khác nhau như thế nào?
Theo Định luật thứ ba của Kepler, bình phương chu kỳ quỹ đạo của một hành tinh tỷ lệ thuận với lập phương bán trục lớn của quỹ đạo elip đó, phản ánh mối quan hệ giữa kích thước quỹ đạo và thời gian để hoàn thành một vòng quay.
Câu hỏi 5: Tại sao quỹ đạo của các hành tinh lại không phải là hình tròn?
Trong không gian, vận tốc của các hành tinh biến đổi liên tục, không đảm bảo sự ổn định cần thiết cho một quỹ đạo tròn hoàn hảo. Do đó, sự thay đổi nhỏ trong vận tốc có thể gây ra sự chuyển động theo quỹ đạo elip, thay vì một vòng tròn đơn giản.
Hy vọng qua bài viết này tại thienvanhoc.edu.vn, bạn đã có thể hiểu sâu sắc hơn về ba Định luật Kepler và tầm quan trọng của chúng trong việc hình thành lý thuyết về chuyển động của các hành tinh. Những kiến thức này không chỉ là cơ sở để phát triển các nghiên cứu thiên văn và vật lý hơn nữa mà còn mở ra cánh cửa hiểu biết về vũ trụ rộng lớn mà chúng ta đang sống.
Đừng quên theo dõi chúng tôi để cập nhật thêm nhiều bài viết giáo dục và khoa học khác. Hãy tiếp tục khám phá và mở rộng kiến thức của bạn về vũ trụ với thienvanhoc.edu.vn, nơi cung cấp cho bạn một hành trình đầy cảm hứng và khám phá trong lĩnh vực thiên văn học!
